We can draw three outgoing rays from the pencil and find the point at which an image forms by finding the intersection of these lines. Let's put these principles into practice and inspect some ray diagrams for a pencil reflected in the concave surface of a mirror:ĭiagram 1) Here the pencil is located further from the mirror than the focal length F.
All rays passing through the centre of curvature reflect directly back through it again. its vertex) will reflect at the same angle as their angle of incidence in the same way that all incident rays to a plane mirror do. Any rays which meet the mirror's surface at the optic axis (i.e. By the same token any rays passing through the focal point will reflect parallel to the optic axis. Any rays parallel to the optic axis will reflect through the mirror's focal point, which is found halfway between its centre of curvature and vertex. For spherical mirrors, an optic axis can be drawn from the sphere's centre of curvature to the vertex on the mirror's surface. These graphic representations have a number of important features which, when understood, allow us to predict the properties of an object's image: When describing the formation of images in a mirror it is useful to set up a ray diagram. To explain this phenomenon, we need to understand how rays of light leaving an object form an image en route to our eyes via a reflecting surface. Particularly curious children might notice that their reflected image appears upside down in the concave surface of a spoon but the correct way up in the opposite convex surface. 
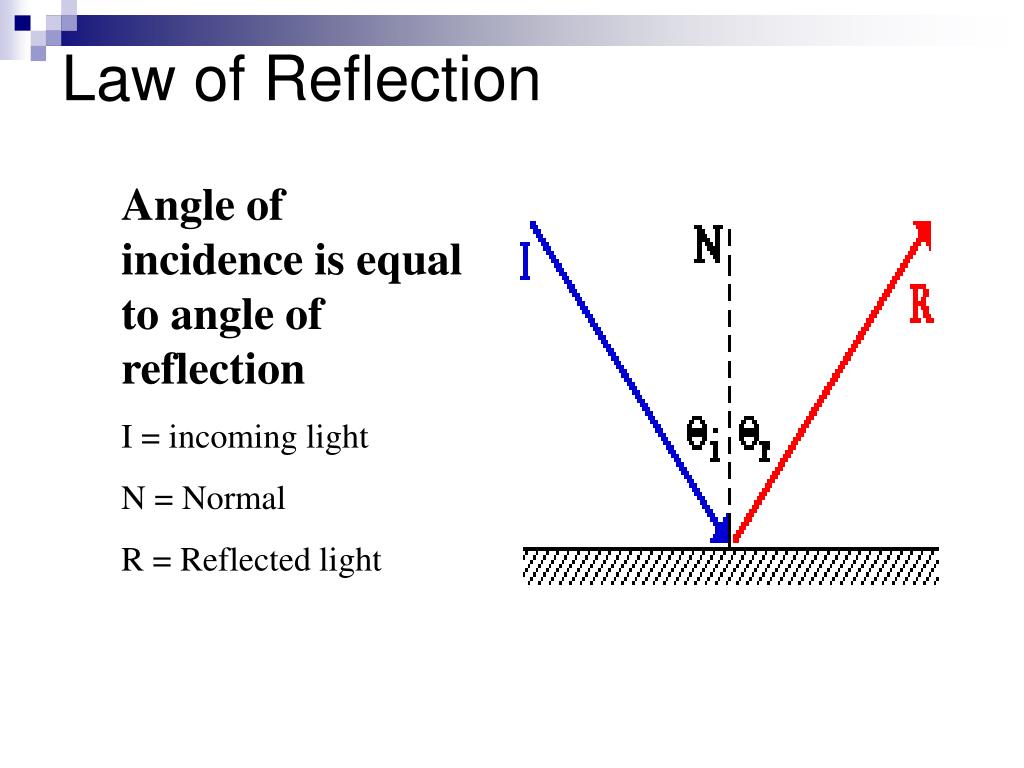
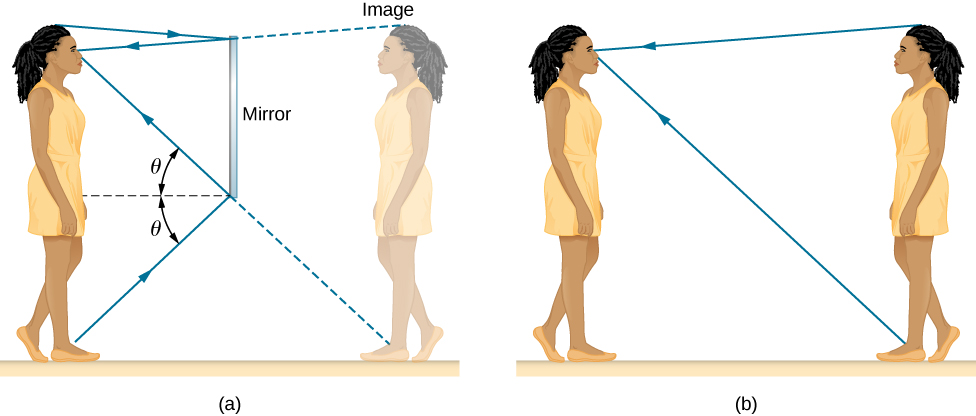
However, any reflecting surface, planar or otherwise, can act as a mirror, and this is why many baubles and lenses are 'shiny'.Įven the humble cereal spoon can act as a type of spherical mirror, which many of us discover as children procrastinating at the breakfast table. When you think of a mirror, chances are you picture a typical bedroom 'plane mirror'.
0 kommentar(er)
